Tuesday, October 26

Life annuity value

In actuarial science, the actuarial present value of a payment or series of payments which are random variables is the expected value of the present value of the payments, or equivalently, the present value of their expected values.

Actuarial present values are calculated for the payment or series of payments associated with life insurance and life annuities. In this case, the probability of a future payment is based on assumptions about the person's future mortality taking into account the person's age and an assumed life table, while the present value of those future assumed payments depend upon the interest rate (or rates) used to discount them for the passage of time.

The internal rate of return of a contract is the rate of return for which the actuarial present value of all cash flows is zero.

Life insurance

Let T be the future lifetime random variable of an individual age x and Z be the present value random variable of a whole life insurance benefit of 1 payable at the instant of death.
\,Z=v^T=(1+i)^{-T}=e^{-\delta T}
where i is the interest rate and δ is the equivalent force of interest.
To calculate the actuarial present value we need to calculate the expected value \,E(Z)=E(v^T) of this random variable Z. For someone aged x this is denoted as \,\overline{A}_x\! in actuarial notation. It can be calculated as
\,\overline{A}_x\! = E(v^T) = \int_0^\infty v^t f_T(t)\,dt = \int_0^\infty v^t\,_tp_x\mu_{x+t}\,dt
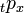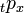where fT is the probability density function of T, \,_tp_x\! is the probability of a life age xx + t and μ denotes force of mortality. surviving to age
The actuarial present value of an n-year term insurance policy can be found similarly by integrating from 0 to n.
The actuarial present value of an n year pure endowment insurance benefit of 1 payable after n years if alive, can be found as
\,_nE_x = P(T>n)v^n = \,_np_xv^n.
In practice the best information available about the random variable T is drawn from life tables, which give figures by year. The actuarial present value of a benefit of 1 payable at the birthday after death would be
\,A_x = \sum_{k=0}^\infty v^{k+1} P(k<T<k+1) = \sum_{k=0}^\infty v^{k+1} \,_kp_xq_{x+k}
where \,q_x\! is the probability of death between the ages of x and x + 1.
In practice an insurance policy pays soon after death, which requires an adjustment of the formula.

Life annuity

The actuarial present value of a life annuity of 1 per year paid continuously can be found in two ways:
Aggregate payment technique (taking the expected value of the total present value):
This is similar to the method for a life insurance policy. This time the random variable Y is the total present value random variable of the life annuity of 1 per year paid continuously as long as the person is alive, and is given by:
Y=a_{\overline{T|}} = \frac{1-(1+i)^{-T}}{\delta} = \frac{1-v^T}{\delta}.
The expected value of Y is:
\,\overline{a}_x = \int_0^\infty a_{\overline{t|}} f_T(t)\,dt = \int_0^\infty a_{\overline{t|}} \,_tp_x\mu_{x+t}\,dt
Current payment technique (taking the total present value of the function of time representing the expected values of payments):
\,\overline{a}_x =\int_0^\infty v^{t} (1-F_T(t))\,dt= \int_0^\infty v^{t} \,_tp_x\,dt\,
where F(t) is the cumulative distribution function of the random variable T.
The equivalence follows also from integration by parts.
In practice life annuities are not paid continuously. If the payments are made at the end of each period the actuarial present value is given by
a_x = \sum_{k=1}^\infty v^k (1-F_T(k)) = \sum_{k=1}^\infty v^k \,_kp_x.
Keeping the total payment per year equal to 1, the longer the period, the smaller the present value is due to two effects:
  • The payments are made on average half a period later than in the continuous case.
  • There is no proportional payment for the time in the period of death, i.e. a "loss" of payment for on average half a period.
Conversely, for contracts costing an equal lumpsum and having the same internal rate of return, the longer the period between payments, the larger the total payment per year.

Life insurance as a function of the life annuity

The value of a life insurance can be derived from the value of a life annuity-due this way:
\,A_x = 1-iv \ddot{a}_x
This is also commonly written as:
\,A_x = 1-d \ddot{a}_x
The formula also works equally well in the continuous case. In the case where the annuity and life insurance are not whole life, one should replace the insurance with an n-year endowment insurance (which can be expressed as the sum of an n-year term insurance and an n-year pure endowment), and the annuity with an n-year annuity due.

See also


(source:wikipedia)
Posted by at
Labels:

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)